Optimal Transport for Offline Imitation Learning

With the advent of large datasets, offline reinforcement learning (ORL) is a promising framework for learning good decision-making policies without interacting with the real environment. However, offline RL requires the dataset to be reward-annotated, which presents practical challenges when reward engineering is difficult or when obtaining reward annotations is labor-intensive. However, abundant unlabeled data may be available for offline learning, which motivates the question: how can we leverage unlabeled data for offline RL?

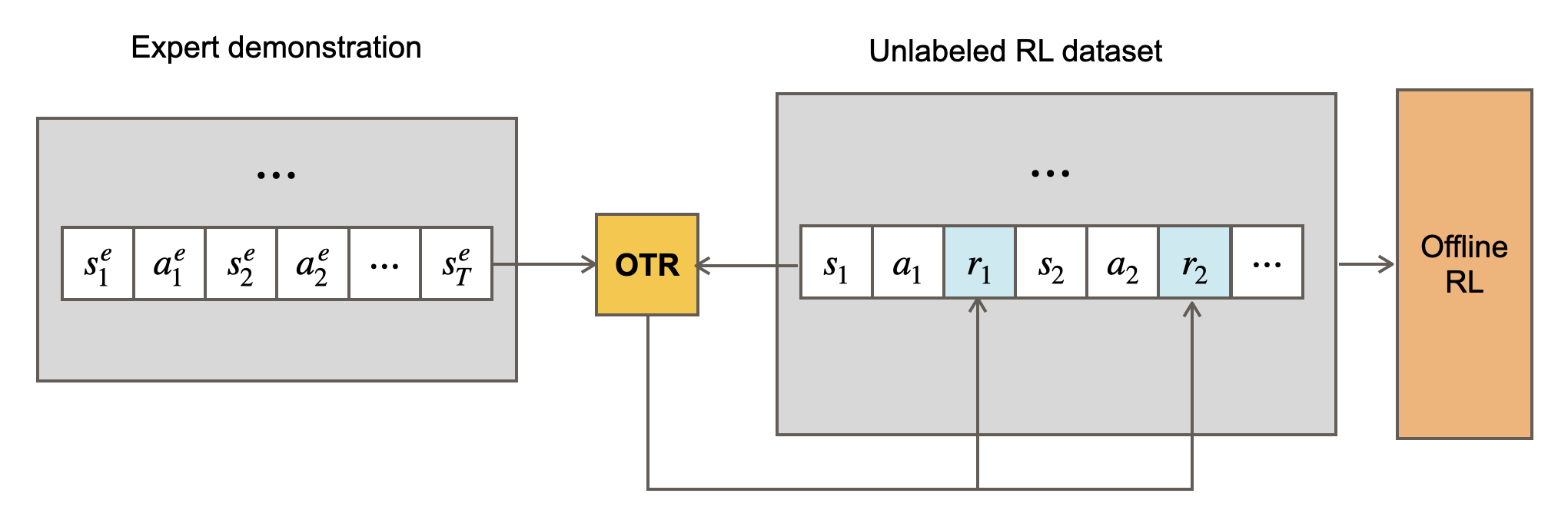
In our recent paper at ICLR 2023, we introduce Optimal Transport Reward labeling (OTR), an algorithm for assigning unlabeled trajectories with rewards. OTR enables unlabeled trajectories to be used as if they have been reward-annotated, enabling the offline agents to take full advantage of the offline data available.

Background

Learning from offline experience has become an increasingly popular topic in the reinforcement learning (RL) community due to the challenges in sample complexity with online RL. Behavior Cloning (BC)¹ is a popular approach for learning from offline data. However, BC requires a large amount of expert demonstrations to work well in practice, which can be difficult for applications where collecting expert demonstrations is expensive.

Offline reinforcement learning (ORL)² has gained much traction in recent years thanks to its ability to learn policies from previously collected data without further environmental interaction. This approach is particularly useful in cases where data collection can be expensive or slow, such as robotics, financial trading, and autonomous driving. Furthermore, unlike online RL, offline RL can learn an improved policy beyond demonstrations in the dataset. However, offline RL methods require a reward function to label the logged experience, which can be impractical in applications where rewards are hard to specify with hand-crafted rules. Even if human expertise can be used to label the trajectories, generating reward signals this way can be costly. As such, the ability of offline RL to leverage unlabeled data remains an open question of significant practical value.

Optimal Transport Reward labeling (OTR)

For offline RL algorithms to leverage the unlabeled experience, we need to assign rewards to the unlabeled trajectories. An intuitive way to think about reward annotation when given a few expert demonstrations is to consider using some measure of similarity between the trajectories in the unlabeled dataset and those in the expert demonstrations as a reward function.

Optimal Transport (OT)³ is a principled approach for comparing probability measures. The (squared) Wasserstein distance between two discrete measures $\mu_x = \frac{1}{T} \sum_{t=1}^T \delta_{x_t}$ and $\mu_y = \frac{1}{T’} \sum_{t=1}^{T’} \delta_{y_t}$ and

$$ \mathcal{W}^2(\mu_x, \mu_y) = \min_{\mu \in M} \sum_{t=1}^{T}\sum_{t’=1}^{T’} c(x_t, y_{t’}) \mu_{t,t’}, $$

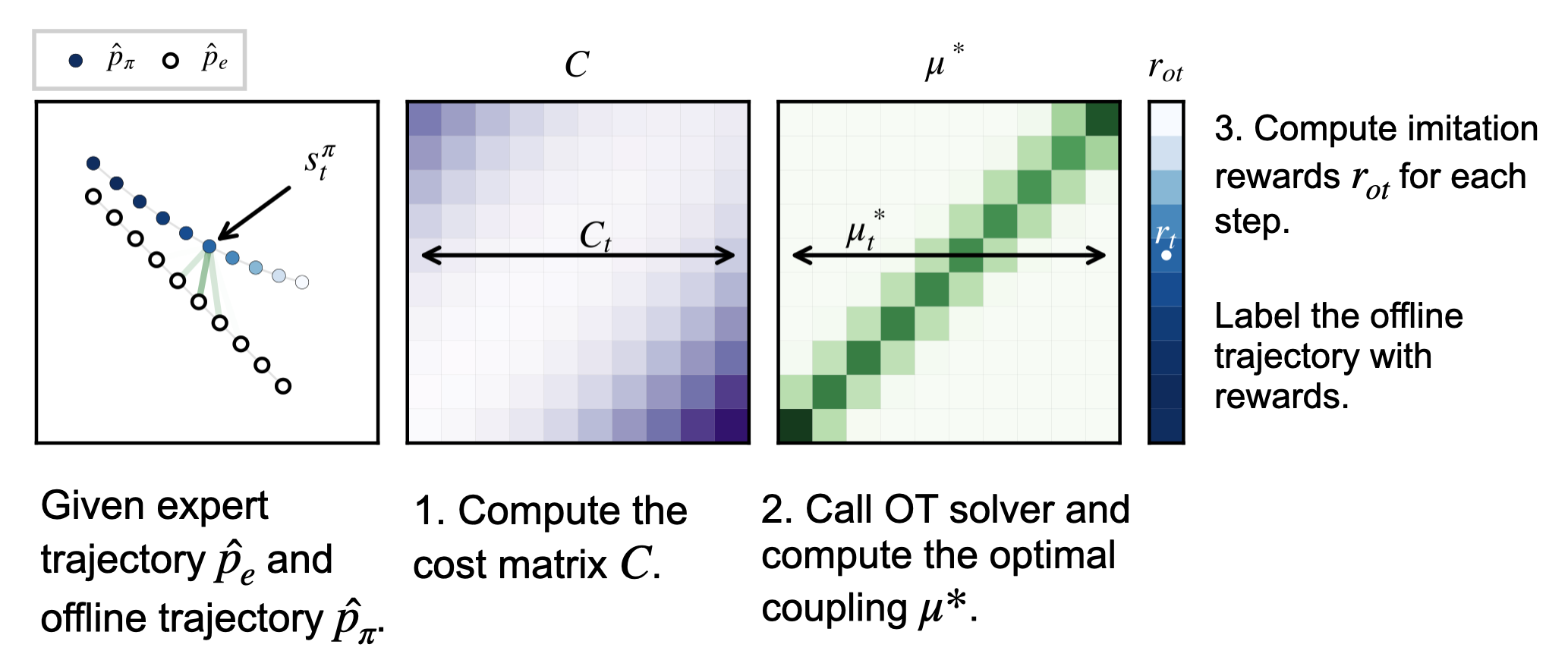
where $M = {\mu \in \mathbb{R}^{T \times T’} : \mu \mathbf{1} = \frac{1}{T} \mathbf{1}, \mu^T \mathbf{1} = \frac{1}{T’} \mathbf{1}}$ is the set of coupling matrices, $c$ is a cost function, and $\delta_x$ refers to the Dirac measure for $x$. The optimal coupling $\mu^*$ aligns the samples in $\mu_x$ and $\mu_y$. Unlike other divergence measures (e.g., KL-divergence), the Wasserstein distance is a metric and it incorporates the geometry of the space.

Let $\hat{p_e} = \frac{1}{T’} \sum_{t=1}^{T’} \delta_{s_t^e}$ and $\hat{p_\pi} = \frac{1}{T} \sum_{t=1}^T \delta_{s_t^\pi}$ denote the empirical state distribution of an expert policy $\pi_e$ and behavior policy $\pi$ respectively. Then the (squared) Wasserstein distance

$$ \mathcal{W}^2(\hat{p}_\pi, \hat{p}_e) = \min _{\mu \in M} \sum _{t=1}^T \sum _{t’=1}^{T’} c(s _t^\pi, s _{t’}^e) \mu _{t,t’} $$

can be used to measure the distance between expert policy and behavior policy. Let $\mu^*$ denote the optimal coupling for the optimization problem above, then we can use the following reward function

$$ r_{\text{ot}}(s_t^\pi) = -\sum_{t’=1}^{T’} c(s_t^\pi, s_{t’}^e) \mu^*_{t,t’}, $$

for learning a policy $\pi$ that imitates the expert policy. This describes the main idea behind OTR: we can use the Wasserstein distance between the empirical state distributions of the expert policy and the unlabeled behavior policy to measure their similarity and use $r_{\text{ot}}$ as a reward function for offline RL. The following figure summarizes the procedure of OTR.

Despite the conceptual simplicity, OTR has several advantages:

1. OTR runs fast, thanks to the availability of high-performance OT solvers and accelerators. labeling a dataset of one million transitions takes two minutes on a single GPU.
2. OTR performs consistently well across various offline datasets and tasks and is data-efficient. For example, on the D4RL benchmarks⁴, we find that OTR matches the performance of offline RL algorithms with oracle rewards given a single episode of expert demonstration.
3. OTR can be used with any offline RL algorithm.

Summary

In conclusion, we present OTR, a simple yet powerful algorithm for labeling offline RL datasets with rewards using a handful of expert demonstrations. Our results show that OTR performs well on popular offline RL benchmarks, even in cases where most reward annotations are unavailable. Finally, you can easily combine OTR with an offline RL of your choice to learn from previously unlabeled data. We invite you to read our paper and try out the open-source JAX implementation on GitHub.

References